Revista nº 798

106 / 88

106 Jose Arturo Molina Mora
Enfermedadde Tarui: revisión y perspectivas bioinformáticas
Como ha sido verificado en diversos casos reportados, ya sea
por la existencia de las mismas mutaciones en la FFQ con diferente
sintomatología entre pacientes, o bien, en el caso de la enfermedad
vista como glucogenosis secundaria, el entendimiento de la enferme-
dad de Tarui es de alta complejidad. Ofrece un desafío para su estudio
que comprende mecanismos regulatorios que no podrían ser expli-
cados únicamente con el estudio de la estructura tridimensional de
forma aislada. Es por ello que una segunda área de la bioinformática
de interés para el estudio de esta EAG es la biología de sistemas, con
la cual se evalúan propiedades que únicamente pueden emerger a
partir del análisis de los sistemas biológicos vistos como un todo y no
como elementos individuales.
Un ejemplo del potencial de la biología de sistemas puede ser
considerado con el modelo matemático presentado por Lambeth y
colaboradores, el cual representa dinámicamente la vía de la glicólisis
hasta la producción de energía y lactato en el músculo esquelético
de mamíferos. El modelo se construyó con parámetros cinéticos ob-
tenidos a partir de la literatura y con restricciones estequiométricas,
balance de masa y con una termodinámica basada en la ley de acción
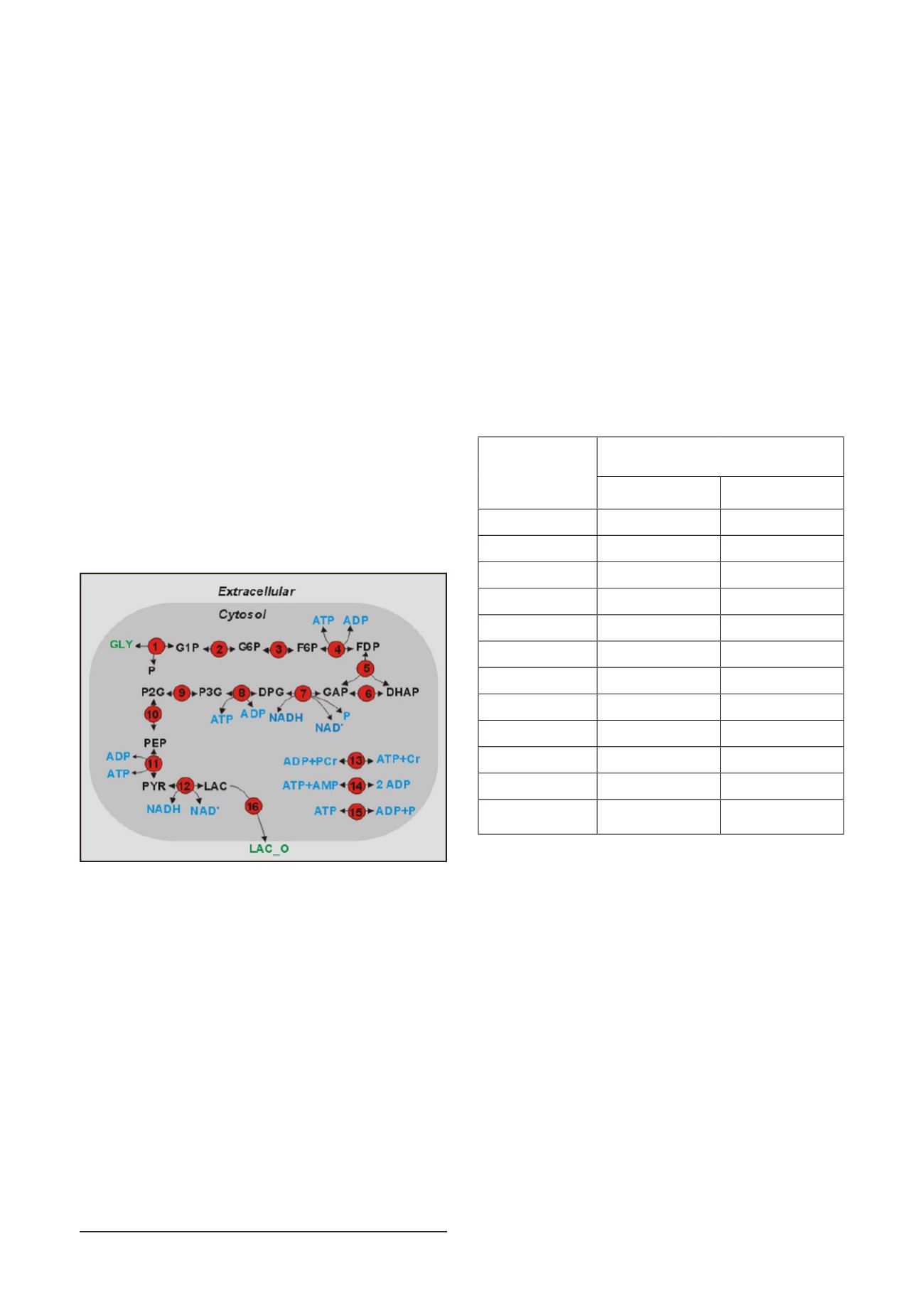
de masas combinada. La topología general es presentada en la Figura
1 (los números en los círculos rojos indica un paso enzimático en el
orden usual de la glicólisis). Los mismos autores mencionan que el
principal resultado del análisis fue el acoplamiento de la vía con la
red de regulación de la ATPasa, haciendo que el sistema en estado
estable sea más sensible a la actividad de ATPasa externa y no a me-
canismos internos de la vía, lo cual permite la interconexión con otras
vías y explica cómo los cambios en la glicólisis logran tener un efecto
en vías alternativas para modular la cinética del ATP en el músculo
esquelético (39).
Con este modelo es posible realizar simulaciones en línea,
incluyendo la enfermedad de Tarui
models/?id=lambeth). Inicialmente, utilizando el sistema de
ecuaciones diferenciales planteado, la constante de reacción del
paso catalizado por la FFQ se redujo a la mitad (Vfpfk, de 0.056 a
0.028), con el objetivo de valorar el efecto en la producción de los
metabolitos finales del modelos, NADH (el valor bajó a un 9% del
normal) y piruvato (el valor bajó a un 60% del normal). Estos dos
metabolitos son particularmente relevantes en el contexto de la
fisiopatología de la enfermedad, pues el bloqueo de la glicólisis
impide la producción de éstos y su continuidad a rutas metabóli-
cas (aeróbicas o anaeróbicas), lo cual compromete la disponibili-
dad de energía en los tejidos, principalmente músculo. Si existie-
sen otras alternativas para modular la producción, podría usarse
como estrategia para solventar la necesidad energética ante la
deficiencia de la FFQ, y justamente las predicciones in silico del
modelo matemático propone alternativas para ello. Al realizar el
análisis de sensibilidad en el modelo de ecuaciones diferenciales
y con el objetivo de determinar los puntos del modelo que per-
mitan aumentar los valores de dichos productos (ver tabla 3), se
obtuvo que los pasos del modelo donde actúan la piruvato qui-
nasa (PQ, paso V11) y la deshidrogenasa láctica (DHL, paso V12)
fueron los más representativos para reponer los valores del NADH
y piruvato.
En la tabla 3, los valores extremos positivos de los coefi-
cientes de control (rojo, paso V1) indican que la producción de
NADH y piruvato se favorece al incrementar la reacción asocia-
da, mientras que los valores extremos negativos (verde) son lo
que más consumen dichas moléculas. Aunque algebraicamente
aumentar los valores del paso V1 significaría un aumento de los
productos, el bloqueo del paso de la FFQ no tendría efecto. Así,
la inhibición de las reacciones V11 y V12 supondría la disminu-
ción del consumo de NADH y piruvato. En la simulación, la in-
hibición al 50% de cada una de las actividades en la respectiva
constante de reacción, muestra un aumento de NADH al 70%
del normal (enfermo era 9%) y un 95% de piruvato respecto al
normal (enfermo era 60%).
De forma acoplada a otras vías de regulación, esto indica-
ría que puede modularse la actividad o la cinética asociada a las
enzimas piruvato quinasa y deshidrogenasa láctica para repo-
ner la producción de energía de forma alternativa para contra-
rrestar los efectos en la enfermedad de Tarui. En este sentido,
aspectos como el redireccionamiento de la fuente de energía
hacia los lípidos o el flujo de carbono a través de la vía de las
pentosas fosfato (1)(9), serían aspectos que podrían estudiarse
como un sistema metabólico que, en conjunto con la FFQ, po-
drían brindar explicaciones referentes a la sintomatología o de
opciones para posibles tratamientos.
Además, en otras posibles líneas de modulación, se ha re-
portado que la activación y la inhibición alostérica de la enzima
por más de diez metabolitos y en respuesta a la señalización hor-
monal resultan en la regulación del flujo glucolítico para satisfacer
las necesidades de energía de las células (19). Estos reguladores
Figura 1. Topología del modelo de la glicosis en músculo esquelético.
(Imagen del reposiorio JWS Online ) del
trabajo de Lambeth & Kushmerick, 2002).
Flujo
Coeficientes de control
NADH PYR
V1 0.72654002 0.28313945
V2 0.16379237 0.06383142
V3 0.0155692 0.00606746
V4 (FFQ) 0.62511484 0.24361311
V5 0.03698243 0.0144124
V6 0.00202692 0.00078991
V7 0.0050729 0.00197696
V8 0.0198994 0.00782085
V9 -0.26547427 0.07306843
V10 -0.56865805 0.15319517
V11 (PQ) -0.72578393 0.19415981
V12 (DHL) -0.03508182 -1.04207497
Tabla 3. Coeficientes de control para NADH y piruvato en el modelo
matemático.
Fuente: Repositorio JWS Online ,
Lambeth & Kushmerick, 2002 (39)