
130
Francisco Javier Moreno Rodríguez
Los outliers en los grupos diagnósticos relacionados
DISCUSIÓN
Es clásica la definición de outlier de Hawkins, calificada por
él mismo de intuitiva. A la pregunta sobre qué es un outlier, Haw-
kins responde que “sería una observación que se desvía tanto de
otras observaciones como para despertar sospechas de que fue
generada por un mecanismo diferente” (12). Los métodos esta-
dísticos paramétricos de detección de outliers parten del supues-
to de una distribución de los datos conocida, que generalmente
es una distribución Normal, y se basan en estimaciones estadísti-
cas de los parámetros de la distribución. En general, la media y la
varianza de la muestra dan una buena estimación de la distribu-
ción de los datos. Pero cuando la base de datos está contaminada
por outliers, esos estimadores pueden desviarse, pues son alta-
mente sensibles a los valores extremos. Se dice entonces que son
estimadores poco robustos (13). Tukey abordó en 1977 el proble-
ma de los estimadores robustos e introdujo el diagrama de caja
(boxplot) en el análisis exploratorio de datos (14). El diagrama de
caja es una representación gráfica basada en la distribución de los
cuartiles, en la que los valores atípicos aparecen remarcados. Los
cuartiles primero (Q1) o percentil 25 y tercero (Q3) o percentil 75
se utilizan para obtener una medida robusta de variabilidad, el
rango intercuartílico (Q3 – Q1), que puede sustituir a la desvia-
ción típica (DT), mientras que el cuartil segundo o mediana se usa
como una medida robusta de centralización, en lugar de la media.
El gráfico de caja y bigotes proporciona una representación de la
distribución de la variable en la que los límites inferior y superior
de la caja corresponden a los cuartiles primero y tercero, respec-
tivamente, coincidiendo por tanto la altura de la caja con el rango
intercuartílico. La línea horizontal dentro de la caja corresponde
a la mediana y los bigotes inferior y superior al mínimo y máximo
valor tales que su distancia a los límites inferior y superior de la
caja sea igual a 1,5 (Q3 – Q1). Los puntos de corte son entonces
Q1 – 1,5 (Q3 – Q1) y Q3 + 1,5 (Q3 – Q1), más allá de los cuales las
observaciones serán consideradas valores atípicos. El coeficiente
1,5 se elige por las características propias de la distribución Nor-
mal, ya que para una gran muestra de una población con este
tipo de distribución los puntos de corte deben estar cercanos a
la media ± 2,67 DT y sólo alrededor del 0,8% de los datos serán
observaciones atípicas (14,15).
La metodología descriptiva de los datos propuesta por
Tukey mediante el diagrama de caja es adoptada por M. Casas
en 1991 para la detección y eliminación de las altas con valores
atípicos de estancia hospitalaria en el sistema de clasificación
de pacientes de los GRD. Casas afirma que “un GRD puede con-
tener algunas observaciones con valores muy prolongados de
estancia. Estas observaciones tienen la capacidad de alterar los
estadísticos del conjunto de los datos, en especial la media arit-
mética – la estancia media – y las medidas de dispersión. Por
consiguiente, respecto a estas observaciones es de interés su
detección y exclusión, para la caracterización sin distorsiones de
los estadísticos del conjunto restante” (2). Y señala, sin citar la
referencia del diagrama de caja de Tukey como fundamento ori-
ginario de su método, que “la detección y posterior exclusión se
realiza mediante el procedimiento de ‘trimming’ (depuración),
que determina los puntos de corte fuera de los cuales los ca-
sos se consideran observaciones atípicas” (2). Pero el objetivo
de Tukey era identificar las observaciones que se encuentran
en la llamada “zona outlier” o región de valor atípico y no su
eliminación, que de ningún modo puede hacerse integralmen-
te para todos los datos atípicos mediante la depuración masiva
propuesta por Casas, pues es preceptivo para ello un procedi-
miento específico que sucesivamente someta a cada una de
las observaciones atípicas a una prueba de hipótesis para ser
considerada outlier, empezando por la observación que más
diste de la media (12,14,16,17). En el proceso de depuración
de cada GRD, Casas utiliza solamente el punto de corte supe-
rior del diagrama de caja Q3 + 1,5 (Q3 – Q1), indicando que
“todas las observaciones cuya estancia supera el valor de corte
se consideran observaciones extremas atípicas (outliers) y son
excluidas para el cálculo de estadísticos sobre las observaciones
restantes (estadísticos depurados)” (2). Sin embargo, la mera
aplicación de un solo punto de corte unilateral supone implíci-
tamente la aceptación de la asimetría de la distribución de las
estancias hospitalarias, lo cual es contradictorio con la hipótesis
de Normalidad en que se basan la detección y eliminación de los
outliers (12,14,17).
El método de Casas ha sido admitido en España de forma
acrítica por todo tipo de organismos oficiales, autonómicos y na-
cionales, incluido el Ministerio de Sanidad. En las dos ediciones
de los indicadores clave del SNS se asume el criterio de excluir
los llamados casos extremos en el cálculo de los indicadores de
casuística y funcionamiento hospitalarios. Aunque, bien es ver-
dad, con una nota oficial complementaria: la de añadir al punto
de corte superior, establecido para la detección y eliminación
de los valores atípicos superiores, un punto de corte inferior
opuesto, para la detección y eliminación asimismo de los valo-
res atípicos inferiores (6,7). Esta aportación ministerial es lógica
y pretende dotar de coherencia interna al sistema de detección
y eliminación de los casos extremos, si bien la prueba informal
de Normalidad que habitualmente supone la aplicación bilateral
de los puntos de corte del diagrama de caja viene a mostrar de
modo fehaciente la asimetría de la distribución de las estancias
hospitalarias, ya que regularmente el 99,9% de los casos extre-
mos son valores superiores. Es ilustrativo a este respecto que en
la norma estatal del año 2009 los puntos de corte inferiores, ob-
tenidos mediante la fórmula Q1 - 1,5 (Q3 – Q1), señalan valores
positivos de estancia solamente en 13 de los 676 GRD (10). Las
fórmulas de los puntos de corte están basadas en el supuesto de
una distribución Normal de los datos. Pero esta premisa no se
cumple en el caso de las estancias hospitalarias, ya que la curva
de su distribución es asimétrica, con una cola hacia la derecha
más prolongada. Ello se debe a que el límite inferior de la es-
tancia es un día - aunque se incluyen en el CMBD determinadas
altas con estancia de cero días (18) – no habiendo, en cambio,
límite superior para la duración de la misma, que puede exten-
derse de forma ilimitada, con el consiguiente sesgo positivo de
sus valores (19). Si la distribución de las estancias hospitalarias
fuera Normal, la exclusión de los casos extremos no supondría
una variación sustancial en la estimación puntual de la EM, de-
bido a la simetría que caracteriza a ese tipo de distribución. Pero
el sesgo positivo de los datos convierte a los casos extremos
superiores, de modo sistemático, en valores influyentes sobre
un estimador tan poco robusto como la media, a la que una
sola observación puede hacer variar considerablemente (20).
Por ello, el efecto de la eliminación de los casos extremos, que
representan más de un 5% de las altas hospitalarias del CMBD,
es una gran disminución de la varianza de las estancias y una
importante subestimación de la media.
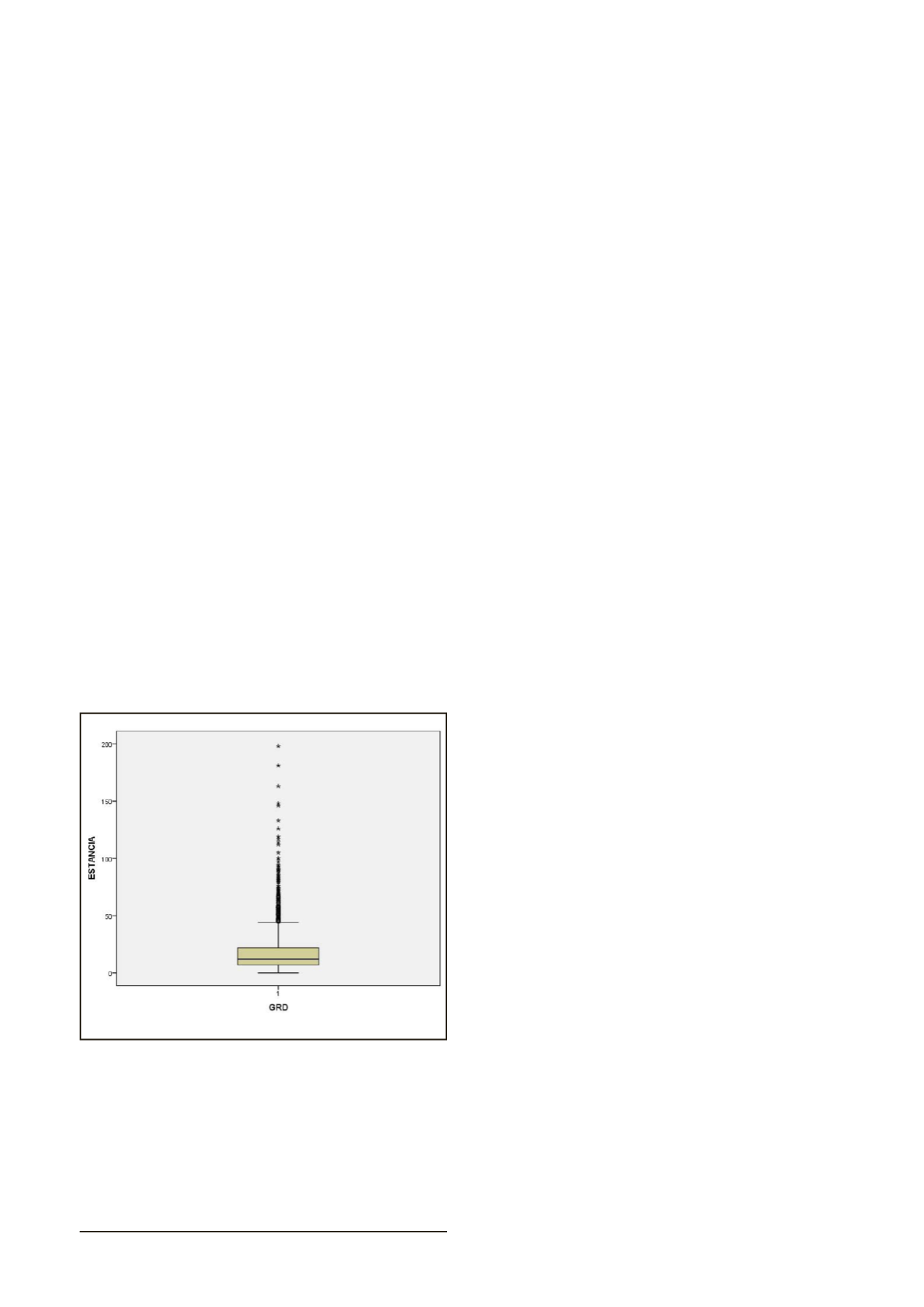
Gráfico 2. Diagrama de caja del GRD 1: Craneotomía edad >17 con
complicaciones. CMBD 2009

















